2022년 CVPR에서 공개된 High-Resolution Image Synthesis with Latent Diffusion Models을 리뷰해보도록 하겠습니다. 최근 생성형 AI, 그 중에서 텍스트를 이용하여 이미지를 생성하는 대표적인 모델인 스테이블 디퓨전(Stable Diffusion)을 공개한 논문입니다.
최근 들어 생성형 AI가 상당히 많은 주목을 받고 있습니다. 자연어 쪽을 우선 살펴보면 LLM, 대규모 언어 모델 기반의 생성형 AI들이 생겨나고 그 중 ChatGPT, Bard 등의 모델들이 떠오르면서 이제는 ChatGPT가 없으면 불편해질 정도가 되어버렸습니다.
이미지 생성 모델 역시 계속적인 발전을 이루고 있습니다. GAN이 떠오르면서 StyleGAN + CLIP 등 신기한 아이디어들이 나오더니, 결국은 DALL-E 2 등 상당히 좋은 이미지 생성 모델이 나타나고 있는 상황입니다. 그 중 오픈소스로 공개하기도 했고, 성능도 좋고, 리소스마저 적게 먹어 누구나 쓸 수 있어서 너무나 유명해진 모델인 스테이블 디퓨전(Stable Diffusion)을 알아보도록 하겠습니다.
Diffusion Model

디퓨전 모델(Diffusion Model)은 2015년에 처음으로 제안된 아이디어입니다. 위의 그림 중 맨 아래의 그림이 디퓨전 모델인데요. $x_0$ 부터 시작하여 latent space인 $z$ 또는 $x_T$까지 순차적으로 노이즈를 적용한 후, 이를 다시 순차적으로 제거하는 방법으로 모델을 학습하는 방법을 사용합니다.
그림으로 예를 들면 다음과 같이 표현할 수 있습니다. 디퓨전 모델의 Forward, Reverse Process인데요.

왼쪽에서 오른쪽으로 진행되는 Forward Diffusion Process는 $x_0$ 인 이미지 원본부터 $x_T$까지 고정된 가우시안 분포로 생성된 노이즈가 더해진다고 보시면 되며, 이렇게 latent vector를 생성한 후에는 Reverse Diffusion Process를 통해 원본 이미지의 확률 분포와 유사하게 만들게끔 노이즈를 빼는 방식으로 진행됩니다. 이 때의 분포도 정규 분포이지만 위의 고정 정규분포와는 다르게 학습 가능한 파라미터를 사용하여 정규 분포를 학습합니다. 즉 Reverse Process에서만 학습을 수행한다고 볼 수 있습니다.
여기서 $x_0$ 이미지에서 노이즈를 추가하여 $x_T$로 가는 과정을 Forward Process라고 하는데요. 이 과정 중 하나는 정규분포를 가정하기 때문에 다음과 같은 수식으로 정리할 수 있습니다.
$$
q(x_t|x_{t-1}):=\mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_tI)
$$
여기서의 $\beta_t$는 각 단계에서 노이즈를 얼마나 추가할 지 결정하는 상수라고 볼 수 있습니다.
이렇게 정의된 개별 분포를 순서대로 모두 진행해야 하기 때문에 전체 포워드 프로세스는 다음과 같이 정의할 수 있습니다.
$$
q(x_{1:T}|x_{0}):=\prod^T_{t=1}q(x_t|x_{t-1})
$$
디퓨전 모델은 이 Forward Process를 역으로 수행하는 과정을 학습합니다. 역으로 수행하는 과정을 Reverse Process라고 하는데요. 이 과정중 하나는 다음과 같이 정의할 수 있습니다.
$$
p_\theta(x_{t-1}|x_t):= \mathcal{N}(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta(x_t,t))
$$
이 하나의 과정이 $q(x_{t-1}|x_t)$와 최대한 유사하게끔 학습이 진행된다고 보시면 됩니다.
정확한 설명을 위해서는 Loss식을 구하는 과정과 식에 대한 설명이 필요한데요. 이 수식이 상당히 어렵기 때문에 스테이블 디퓨전 논문 리뷰에서는 이정도만 설명하고 향후 DDPM 논문에서 자세히 설명하도록 하겠습니다.
이러한 방법은 DDPM(Denosing Diffusion Probabilistic Model)에서 발전되어 아래와 같이 Reverse Diffusion Process에서는 U-Net 을 사용하게끔 변경되었습니다.

DDPM(Denosing Diffusion Probabilistic Model)은 2020년 발표된 논문으로 사실상 Diffusion Model의 기초 논문이라고 할 수 있는데요. 기존 디퓨전 모델의 Loss의 난잡함도 정리해주고, 새로운 방법도 제시한 중요한 논문이라고 할 수 있습니다. 다만 내용이 너무 많고 어려워서 여기서는 이정도만 소개를 하고 향후에 리뷰를 해보도록 하겠습니다.
참고 : DALL-E 2의 경우 기존 DALL-E의 아키텍쳐 대신 DDPM의 Loss와 디퓨전 프로세스를 채용하여 학습했다고 합니다.
Stable Diffusion
DDPM의 발표 이후 다양한 디퓨전 모델들이 생겼으며, SOTA의 성능을 보여주었는데요. 다만 해상도가 커지면 커질수록 픽셀 하나하나에 대한 연산이 수행되는 디퓨전 모델의 특성상 계산에 필요한 자원이 엄청나게 많이 사용된다는 단점을 해결하지는 못했습니다.
스테이블 디퓨전 이전의 가장 강력한 디퓨전 모델의 경우 학습에 V100 GPU 기준 약 150~1000일 정도의 리소스가 필요했다고 합니다.
연구진은 이러한 문제를 해결하는 것이 목표였는데요. 디퓨전 모델의 성능을 유지하면서도 연산량을 어떻게 줄일 수 있을지에 대해 연구했다고 합니다.
Method

기존의 이미지 생성 모델들을 비교해 본 결과 Rate와 Distortion 간의 trade-off 관계를 확인할 수 있었다고 합니다. 기존 디퓨전 모델들은 눈으로 볼 수 없는 Rate에서 높은 성능을 나타냈다고 하고, 이를 Semantic(의미론적인) compression이라고 표현했습니다. GAN이나 Autoencoder는 Distortion 에서 높은 성능을 보였는데, 이를 Perceptual compression이라고 표현했습니다.
연구진은 이러한 연구 결과를 참고하여 생성 모델을 두 가지 단계로 나누는 방법을 사용합니다. 즉 우선적으로 Perceptual compression을 적용하고, 여기서 얻어낸 Space에서 디퓨전 모델을 적용하는 방법을 제안했습니다. 간단하게 요약하면 다음 그림과 같습니다.

Perceptual Image Compression
Perceptual compression 모델은 오토인코더를 구성하여 학습했는데요. 인코더는 이미지 $x$를 latent space인 $z$로 인코딩하고, 디코더는 $z$를 $~{x}$로 디코딩을 수행합니다.
여기서 latent space의 분산이 커지는 문제가 있어서 이를 정규화하는 실험을 진행했습니다.
- KL-reg: A small KL penalty towards a standard normal distribution over the learned latent, similar to VAE.
- VQ-reg: Uses a vector quantization layer within the decoder, like VQVAE but the quantization layer is absorbed by the decoder.
저는 latent에서 약간의 KL 패널티를 주는 방법과, 디코더 상에서 벡터 양자화 레이어를 통해 정규화를 하는 두 가지 정규화 방법을 사용했다 정도로만 이해했습니다.
오토인코더는 Perceptual Loss와 A patch-based adversarial objective를 사용하여 학습을 수행했는데요.
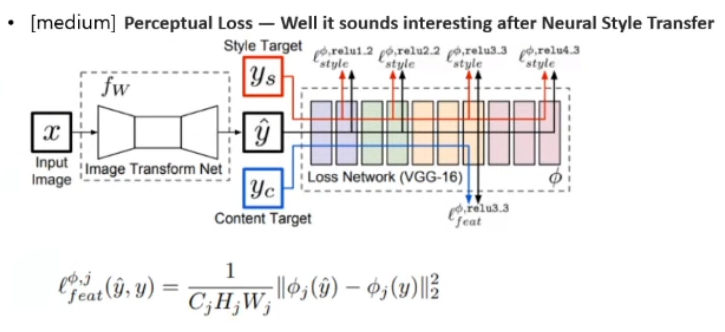
Perceptual Loss는 네트워크 상에서 얻는 피쳐맵마다 거리계산을 하는 방식입니다.
A patch-based adversarial objective라는 방식은 PatchGAN에서 쓰던 방법으로, 이미지 전체를 사용하지 않고 Patch 별로 나누어 이 Patch 이미지가 원본이라고 볼 수 있는지를 True/False로 판단하는 방법이라고 하며, 이 방식을 사용했을 경우 픽셀 단위로 Loss를 보는 것이 아니기 때문에 기존에 나타나던 Blurriness 현상을 완화시킬 수 있었다고 합니다.
여기서 설명하는 방식은 PatchGAN의 Discriminator 부분과 유사한데요. Discriminator가 없는데 어떻게 구현해서 이를 목적함수로 사용했는지는 코드를 살펴봐야 확실하게 알 수 있을 것 같습니다.
Latent Diffusion Models
일반적인 디퓨전 모델의 Loss는 다음과 같이 설명할 수 있는데요.

이를 오토인코더를 사용하여 latent space에 적용했기 때문에 스테이블 디퓨전의 LDM의 Loss는 다음과 같이 표현할 수 있습니다.

여기서의 $\epsilon_\theta(z_t,t)$는 time-conditional한 U-Net을 의미합니다.
Conditioning Mechanisms
마지막으로 Conditioning Mechanisms을 알아보겠습니다. 스테이블 디퓨전 이전의 디퓨전 모델들에는 다양한 Conditioning 과의 결합에 대한 연구가 없었다고 하는데요. 스테이블 디퓨전은 cross-attention을 사용하여 다양한 조건을 사용할 수 있게끔 만들었습니다.
Conditioning이란 텍스트나 이미지 등의 추가적인 표현을 의미한다고 볼 수 있습니다. 예로, 텍스트가 조건으로 들어갈 경우가 요즘 자주 보이는 text-to-image 모델입니다.
먼저 각각의 새로운 조건들을 $y$라고 했을 때, 이를 각 단계에 매핑하기 위해 $\tau_\epsilon(y)\in \R^{M\times d_\tau}$ 로 보내는 인코더 $\tau_\epsilon$을 설정하고, 이를 cross-attention layer를 통해 U-Net의 중간 레이어에 매핑시킵니다.
여기서의 크로스 어텐션 매커니즘은 Query는 기존 $z_t$의 값을, Key와 Value는 $\tau_\epsilon(y)$의 값을 가져오는 전형적인 방법입니다. 즉 식으로 표현하면 다음과 같이 표현할 수 있습니다.
$$
Attention(Q,K,V) = softmax({{QK^T}\over{\sqrt{d}}}V) \
Q = W^{(i)}_Q\phi_i(z_t),\ K=W_K^{(i)}\tau_\theta(y),\ V=W_V^{(i)}\tau_\theta(y),
$$
여기서 $\phi_i(z_t)$는 U-Net의 중간 단계를 표현한다고 보시면 됩니다.
conditional LDM의 Loss는 다음과 같이 표현할 수 있습니다.

Architecture
지금까지 설명드린 내용을 정리하면 다음과 같이 표현할 수 있습니다.

Experiments
마지막으로 실험 결과를 확인해보도록 하겠습니다.

위의 사진은 여러가지 데이터셋에 대해 생성을 진행해 본 결과인데요 상당히 좋은 품질의 데이터가 생성된 것을 확인할 수 있습니다.

수치로도 확인해보도록 하겠습니다. 각각의 데이터셋에 대한 unconditional task(이미지 복원)을 한 결과에 대한 표인데요. CelebA-HQ에서 FID 기준으로 SOTA를 달성한 것을 확인할 수 있습니다. 다만 다른 데이터셋에서는 조금은 낮은 성능을 보이고 있네요.

참고로 계속해서 나오는 평가지표인 FID는 Inception-V3 모델을 사용하여 이미지의 피쳐맵을 추출하고, 이 피쳐맵간의 거리를 계산하는 방법으로 점수를 매기는 방법입니다.
텍스트 조건부 이미지 생성 태스크에서도 꽤 좋은 성능을 보이고 있는데요. GLIDE(OpenAI), Make-A-Scene(Meta)가 더 높은 성능을 보이고는 있으나 파라미터 수를 확인해보면 상당히 가벼움에도 비슷한 성능을 보이고 있다는 장점을 확인할 수 있습니다.

실제로 생성한 이미지를 보면 상당히 고품질의 이미지를 생성했다는 걸 확인하실 수 있습니다.
이외에도 논문을 살펴보시면 layout-to-image, super-resolution, inpainting 등 다양한 태스크에서 좋은 성능을 보이는 걸 확인하실 수 있습니다.
후기
이미지 생성형 AI의 대표적인 모델인 스테이블 디퓨전에 대해 알아보았습니다. 이 모델은 다양한 분야에서 SOTA를 달성한 것도 놀랍지만, 상당히 많은 개발 비용이 들었을텐데도 불구하고 모두 오픈소스로 공개함으로써 일반인들도 사용하게끔 배포한 저자들도 놀랍다는 생각이 듭니다.
오픈소스로 공개함으로써 다양한 사람들이 인공지능으로 현재도 그림을 그리고 있으며, LoRA나 기타 방법을 통한 다양한 미세조정 모델들이 계속해서 공개되고 있습니다.

위의 그림은 스테이블 디퓨전으로 생성한 사실적인 이미지라고 하는데요. 아마 가끔 인터넷에 보이던 AI 그림들의 대부분은 스테이블 디퓨전의 그림이 아닐까 생각되네요.
4GB 정도의 VRAM만 있으면 쉽게 생성할 수 있다고 하니 혹시 Stable Diffusion이 궁금하신 분들은 아래 링크가 좀 자세히 적혀 있는 것 같으니 참고해보시면 좋을 것 같습니다.
Stable Diffusion 인공지능 이미지 생초보 가이드
Stable Diffusion 인공지능 이미지 생초보 가이드
이 글은 Stable Diffusion 또는 다른 이미지 생성형 AI에 대해 거의 아무것도 알지 못하는 초보자를 위한 안내서입니다. (예전에 써둔 글을 새로운 내용을 추가하고 일부 수정하였습니다) 이 글은 스
www.internetmap.kr
