기존 CNN 모델들의 경우 고성능 컴퓨터에서는 이를 연산할 만한 충분한 컴퓨팅 자원들이 있었지만 스마트폰이나 기타 기기에서 사용하기에는 너무 무겁다는 단점을 가지고 있었습니다.
구글은 이러한 문제를 해결하기 위해 Mobilenet을 개발하였으며, 성능을 최대한 희생하지 않으면서도 모바일 환경에서 구동될만큼 경량화 한 것이 특징입니다.
이번 페이지에서는 Mobilenet V1의 핵심 아이디어 Depthwise Separable Convolution을 간략하게 정리하고, Mobilenet V2, 이 모델의 핵심 아이디어인 Inverted Residuals, Linear Bottlenecks를 정리하도록 하겠습니다.
Depthwise Separable Convolution
Mobilenet V2를 이해하기 전에 Mobilenet V1의 핵심 아이디어인 Depthwise Separable Convolution을 정리해보도록 하겠습니다.
기존 방식, Standard Convolution
우선 기존의 방법(Standard Convolution)을 생각해보겠습니다. 기존 방법은 모든 채널에 대해 필터를 통해 한번에 작업을 진행합니다.
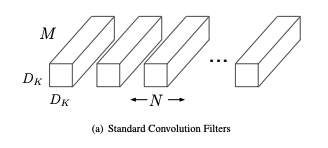
즉 어떤 이미지 X_Y_Z가 존재한다면. 이에 대해 기존 컨볼루전 연산은 $D_K(width) * D_K(height) * M(channel)$ 크기의 필터 $N$개를 이미지에 각각 적용하는 방식입니다.
여기서 나올 수 있는 파라미터 수는 다음과 같이 정리할 수 있습니다. ($D_F$는 피쳐맵의 width, height)
$$
D_K * D_K * M * N * D_F * D_F
$$
그럼 이제 Depthwise Separable Convolution은 어떻게 연산을 수행하는지 살펴보도록 하겠습니다. 우선 Depthwise Separable Convolution은 Depthwise Convolution과 Pointwise Convolution이라는 두 가지 연산으로 나누어져 있습니다.
Depthwise Convolution
인풋된 이미지는 우선 Depthwise Convolution을 수행하게 됩니다. 모든 채널에 대해 바로 필터를 적용하는 기존 방식과는 다르게, Depthwise Convolution은 각각의 채널에 필터를 적용하게 됩니다. 하기 그림을 보시면 필터의 수가 $M$(channel)개인 것을 알 수 있고, 각 채널별로 필터를 적용하기 때문에 필터의 크기도 $D_K * D_K * 1$인 것을 확인할 수 있습니다.
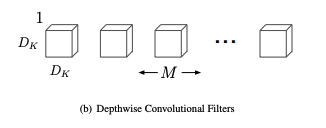
다만 이렇게 연산이 끝날 경우 output으로 나온 피쳐맵의 차원 수가 다르게 됩니다. 따라서 output 차원 수를 맞춰 주기 위한 연산을 해야만 합니다. 이 연산의 파라미터 수는 다음과 같이 정리할 수 있습니다.
$$
D_K * D_K * M * D_F * D_F
$$
Pointwise Convolution
이 연산은 1x1xchannel 크기의 필터를 적용해서 연산량이 적으면서도, output의 width, height는 이전과 동일하고, 채널 수를 필터의 수 만큼 변경하고자 하는 아이디어로 만들어졌습니다.
우리는 Depthwise Convolution으로 나온 $D_F_D_F_M(channel)$ 의 채널 수를 $N$ 개로 변경하는 것이 목적이므로 하기 이미지와 같이 연산을 수행하게 됩니다.
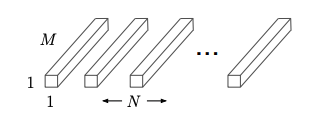
이 연산의 파라미터 수는 다음과 같습니다.
$$
M * N * D_F * D_F
$$
Depthwise Separable Convolution vs Standard Convolution
Depthwise Convolution와 Pointwise Convolution의 파라미터 수를 더해보면 Depthwise Separable Convolution의 최종 파라미터 수를 알 수 있습니다.
$$
D_K * D_K * M * D_F * D_F + M * N * D_F * D_F
$$
이를 정리해보면 다음과 같이 정리할 수 있겠네요.
$$
(D_K * D_K + N) * M * D_F * D_F
$$
그리고 저희는 아까 Standard Convolution의 파라미터를 다음과 같이 정리했습니다.
$$
D_K * D_K * M * N * D_F * D_F
$$
따라서 두 연산간의 차이를 비교해보면 다음과 같이 정리할 수 있습니다.
$$
{Depthwise \over Standard} = {D_K * D_K + N \over D_K * D_K * N} = {1 \over N} + {1 \over D_K * D_K}
$$
대충 3x3 커널을 사용하고 최종 채널을 9개라고 가정해도 4.5배의 차이를 보입니다.
여기서 잠깐 Mobilenet V1의 아키텍쳐를 확인해보도록 하겠습니다.
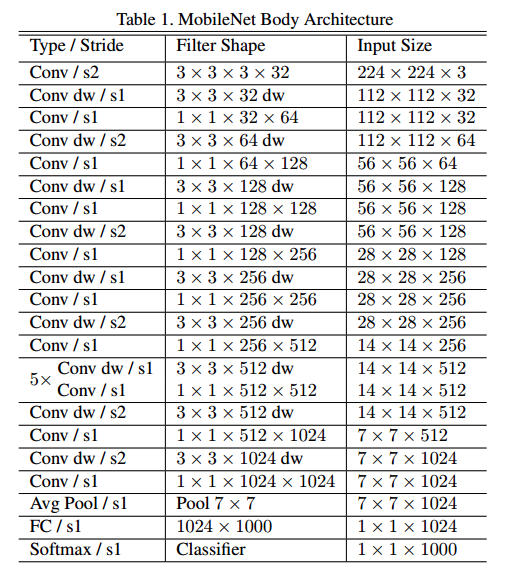
채널 수가 보이시나요? 구조만 바꿧을 뿐인데 정말 어마어마한 연산량 감소를 보여주는 것 같습니다.
참고로 Mobilenet V1은 이 Depthwise Separable Convolution라는 아이디어에 모델의 latency와 accuracy를 조절하는 하이퍼파라미터 두 개를 추가한 구조를 가지고 있습니다. 이제 V1의 핵심 아이디어를 알았으므로 바로 V2의 핵심 아이디어를 살펴보도록 하겠습니다.
Linear Bottlenecks
고차원에서 저차원으로 차원을 감소시킬 때 특징들이 저차원에 매핑이 되는 것을 manifold of interest라고 합니다. 또한 지금까지 연구들에서는 manifold of interest는 저차원 subspace로 embedding이 가능하다고 가정해 왔습니다.
따라서 저자들은 Mobilenet V1에서는 저차원으로 임베딩한 후 다시 고차원으로 복구시키는 방법을 사용했다고 합니다. 다만 ReLU와 같은 활성화 함수로 인해 manifold의 정보가 소실되는 문제가 발생합니다.

다만 위의 그림과 같이 채널이 충분히 많다면 어떤 채널에서는 정보가 살아있을 수는 있다고 합니다.
어쨋든 위의 결론을 다시 한번 곱씹어 보면 다음과 같은 결론을 얻을 수 있습니다.
- manifold of interest에 대해 ReLU를 적용한 후에도 0이 아니라면, 이는 사실 선형 변환과 같다.
추가로 위의 가정(manifold of interest는 저차원 subspace로 embedding이 가능하다.)를 계속 이어가면 다음과 같이 결론을 지을 수 있을 것으로 보입니다.
- manifold of interest의 ReLU값이 계속 양수이면, manifold 상의 정보를 그대로 유지하고 있다고 볼 수 있다.
따라서 저자들은 저차원으로 매핑하는 bottleneck architecture를 만들 때, 선형 변환 역할을 하는 새로운 레이어(Linear Bottleneck Layer)를 만들어서 차원 축소를 하면서도 manifold 상의 중요한 정보들은 그대로 유지하고자 했고, 실제로 ReLU보다 좋은 성능을 보였다고 합니다.
Inverted Residuals
아래 이미지 및 Inverted Residual 설명은 하기 블로그를 참조했습니다.
https://velog.io/@woojinn8/LightWeight-Deep-Learning-7.-MobileNet-v2
우선 일반적인 Residual Bottleneck block을 보도록 하겠습니다.
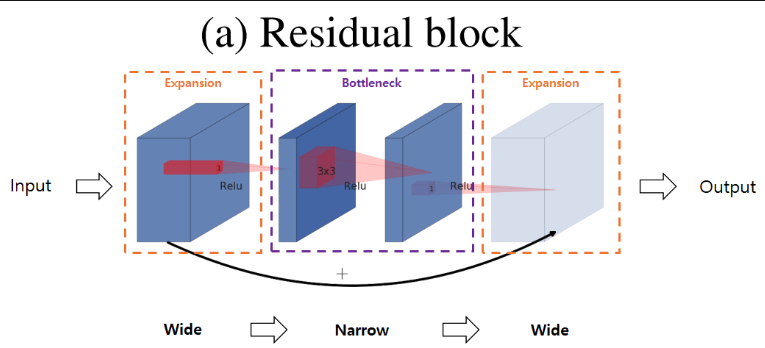
1x1 필터를 통해 bottleneck block를 생성한 후 이를 다시 확장하는 구조로 되어 있습니다. 즉 wide - narrow - wide 구조입니다.
다만 저차원 레이어에 필요한 정보가 압축되어 있다면 연산상의 이점을 가질 수 있도록 반대되는 구조를 만들 수도 있습니다. 이러한 구조가 Inverted Residual block입니다.
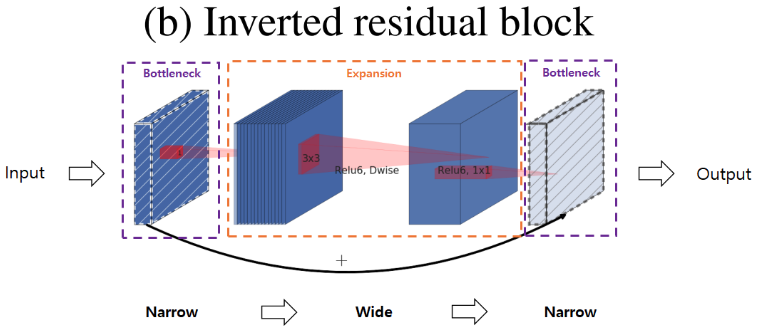
위 그림처럼 narraw - wide - narrow 구조에, narrow끼리 연산을 하는 것을 확인할 수 있습니다. 여기서 빗금이 쳐져 있는 블록은 ReLU를 사용하지 않은 블록입니다.
이렇게 narrrow간 skip connection을 구성한 이유를 다시 설명해보면, 저차원 레이어에 필요한 정보가 압축되어 있다고 가정했기 때문에 이를 skip connection으로 사용해도 정보를 깊은 레이어까지 잘 전달할 것으로 기대할 수 있다고 합니다. 물론 narrrow layer간 연산이기 때문에 연산상에 이점도 존재할 것입니다.
Architecture
Bottleneck Block
우선 Mobilenet에서 사용하는 Convolution block의 구조는 다음과 같습니다. Inverted Residuals에서 본 그 구조입니다.

stride 가 2일 경우에는 skip connection이 구성되어 있지 않으며, 두 연산 다 마지막 컨볼루전 연산은 Linear하다는 특징을 확인할 수 있습니다.

조금 더 상세하게 구조를 보면 t라는 파라미터가 있다는 걸 확인할 수 있습니다. 이 값은 expansion factor
로 불리며 default value는 6입니다.
ReLU6
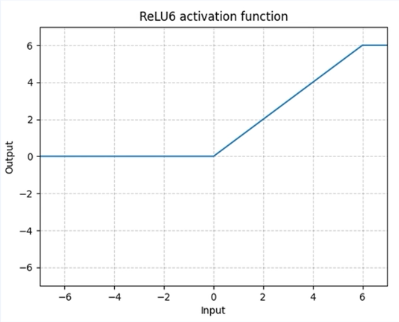
또한 ReLU6라는 활성함수를 볼 수 있는데, 수식은 min(max(0,x),6)이며, 상한을 6으로 두는 활성화 함수입니다. ReLU6의 경우 low precision(적은 bit를 사용한 연산)에 robust하다는 장점이 있다고 합니다.
Mobilenet V2 Architecture
Mobilenet V2의 전체적인 아키텍쳐는 다음과 같습니다.
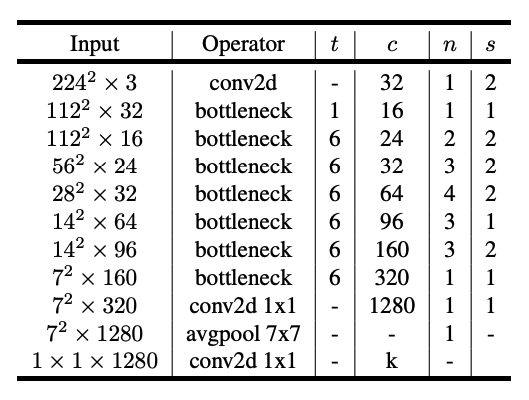
t는 위에서 설명한 expansion factor 입니다.
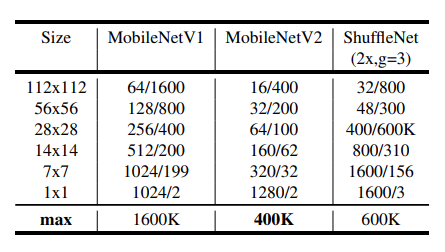
Mobilenet V2는 bottleneck 구조 덕에 이전 모델 대비 1/4의 크기를 만들 수 있었습니다.
