[Head pose] FSA-Net 리뷰

현재 진행중인 프로젝트를 하는 데 있어 Head pose estimating 관련 논문인 FSA-Net 을 알아본 김에 향후 까먹지 않도록 블로그에 리뷰해놓고자 합니다. 데모 파일에 대해 주석처리한 내용도 있어 하단에 링크로 남겼습니다. 글을 작성하는 이유가 제가 까먹지 않기 위한 목적이라 글이 깔끔하지 않을 수 있습니다.

모델 소개

우선 FSA-Net에서 어떠한 결과값이 나오는 지 확인해 보겠습니다.

이미지에 보이는 3가지 선은 Yaw, Pitch, Roll을 활용하여 구현합니다.

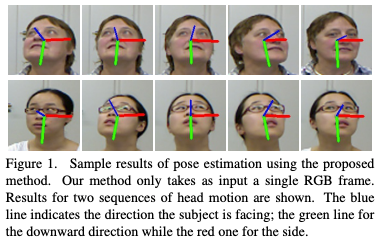
단일 이미지를 Input으로 받았을 때 FSA-Net은 세 가지의 값을 Output합니다. 각각의 값이 Yaw, Pitch, Roll을 의미합니다. Yaw Pitch Roll 정의

Yaw Pitch Roll 정의

다른 기법들은 이런 각도들을 추출하는데 있어, 시간 또는 Depth라는 정보를 포함한 데이터를 받아서 처리를 합니다. 이에 따라 추가적인 연산이 필요하다는 단점이 존재하고, 일부의 경우 일반적인 것이 아닌 특별한 카메라가 필요한 경우도 있습니다. 또한 랜드마크 기반 방식 자체가 얼굴 랜드마크라고 하는 눈,코,입 등에 대해 먼저 예측을 하고 난 후, Head pose를 예측하는 방식이기에 연산량이 많고, 모델의 크기 등이 클 수 밖에 없습니다. FSA-NET의 경우 회귀 기반의 방식으로 이 문제를 해결했고, 이미지 또한 일반적인 이미지로 학습했기에 연산량, 모델의 크기 등에 있어 장점을 가지고 있습니다. 이제 FSA-NET의 구조, 사용하는 기법들에 대해 정리해보겠습니다.

Problem formulation

우선 문제에 대해 정의를 해 보겠습니다. N개의 주어진 데이터를 X, 대응하는 이미지 xn에 대해 맞추고자 하는 포즈 벡터를 yn이라고 정의합니다. 여기서 포즈 벡터 yn은 Yaw, Pitch, Roll이 들어간 3D 벡터입니다. 우리의 목표는 함수 F를 찾는 것이라고 정의하겠습니다. 그러므로 실제 포즈 y에 대해 y˜ = F(x)가 얼마나 맞았는지로 에러를 체크할 수 있습니다. 우리는 회귀 문제로 이를 해결하고자 하므로 MAE를 손실함수로써 다음과 같의 정의할 수 있습니다.

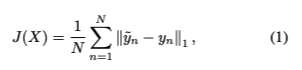
이미지에 대해 연속적인 변수를 예측하고자 회귀 모델링을 하였고, 그 중 MAE를 손실함수로 사용했습니다.

SSR-Net-MD

FSA-Net에서 회귀를 이용한 추정부분은 SSR-Net이라는 논문을 기반으로 만들어졌습니다. 여기서는 SSR-Net이 어떻게 이미지로 연속적인 데이터를 예측할 수 있는지를 보도록 하겠습니다.

SSR-Net은 이미지를 통해 나이를 예측하는 방법을 제안한 논문입니다. 방법을 우선 풀어서 설명하도록 하겠습니다. 이 모델은 나이 추정에 있어 나이를 비닝하여 여러 클래스로 나눠 분류 문제로 변경합니다. 일반적으로 그냥 비닝하는 것이 아닌 coarse-to-fine strategy이라는 전략을 사용하는데, 간단하게 몇 개의 BIN을 만들고, 각각에 대해 확률을 예측하여 그 중 가장 확률이 높은 BIN에서 다시 세부적으로 비닝을 진행하는 방법입니다. 즉, 처음에는 넓게 탐색하다가 점점 더 세부적으로 보는 전략이라고 볼 수 있습니다. 이러한 전략을 SOFT STAGEWISE REGRESSION이라고 하며 이를 약자로 표현하고 사용한 네트워크가 SSR-Net입니다. 나이에 대해 예측하는 예시를 하나 들어보겠습니다.

(1 단계) A : [0–30) B : [30–60) C : [60-90)
(2 단계) A1 : [0–10) A2 : [10– 20) A3 : [20 – 30)
(3 단계) A10 : [0–10)
(최종 집계) 각각의 가중치를 곱하여 결과를 도출함.

SOFT STAGEWISE REGRESSION은 다음과 같이 수식화 할 수 있습니다.

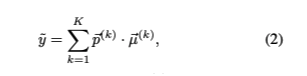
이 수식의 각 기호는 다음과 같습니다.

K : stage의 수
p->(k) : k번째 stage의 확률 분포
mu->(k) : k번째 stage에서 age그룹의 대표 값을 포함하는 벡터

클래스 모호성등을 해결하기 위해 shift vector n->(k), scale vector ∆k가 존재합니다.

n->(k) : 각 bin의 center를 조절
∆k : k번째 stage에서 모든 bin의 너비 조절

이 두개의 벡터는 mu->(k)를 수정합니다. p->(k)처럼 n->(k), ∆k도 네트워크 상에서 출력으로 나오게 됩니다.

즉 어떤 이미지가 들어오면 SSR-Net은 K개의 stage 파라미터 {p->(k), n->(k), ∆k}, 1~K개까지를 출력하게되고, SOFT STAGEWISE REGRESSION(SSR)를 통해 나이를 추정합니다.

SSR, 이를 사용하는 SSR-Net을 굳이 왜 알아야 할까요? FSA-Net이 예측하고자 하는 값이 이미지에서 일반적으로 뽑고자 하는 범주형 변수가 아닌 연속형 변수이기 때문입니다. 대신 일반적인 SSR-Net은 하나의 스칼라 값(여기서는 나이)을 예측하는 모델입니다. 우리는 3D 벡터(Yaw, Pitch, Roll)을 예측해야만 하기 때문에 다차원 회귀와 관련된 SSR-Net-MD라는 모델을 사용하도록 하겠습니다.

Overview of FSA-Net

아직 설명하지 않은 내용들이 있지만, 여기서 먼저 전반적인 Overview를 확인하고 넘어가겠습니다. FSA-Net의 전체적인 플로우는 다음과 같습니다.

우선 이미지가 두 개의 Stream으로 들어가는 걸 확인할 수 있습니다. 이는 랜드마크를 사용하지 않고, 특징을 잘 뽑기 위해 two-stream 구조를 택했다고 정리할 수 있습니다. 하단 부분의 SSR Module을 통해 예측을 수행한다는 점도 확인할 수 있습니다. 사실 two-stream을 포함한 전반적인 구조는 SSR-Net을 그대로 사용했습니다.

다시 처음부터 정리해보면 이미지는 2개의 stream으로 들어갑니다. 이후 3개의 stage를 통과하는 것을 확인할 수 있습니다. 이 과정을 정리해보면,

 

1. 각각의 stream은 각 stage에서 feature map을 추출합니다.
2. 여기서 각각의 stage 수행 이후 추출된 2개의 피쳐 맵을 stage fusion module을 통해 합칩니다.
3. 이 stage fusion module은 각 피쳐 맵을 요소별 곱셈을 취합니다.
4. 그 다음 c 1x1 Convolution을 적용하고, Average pooling을 적용합니다.

이로써 k번째 스테이지의 피쳐 맵 Uk는 w x h x c의 크기를 갖습니다.

정리하자면, 이미지의 특징을 잘 뽑기 위해 2개의 다른 Net으로 특징을 추출했고, 이를 병합하는 과정을 거칩니다.
여기서 Output된 이미지 크기는 원하는 크기인 w x h x c의 크기인 Uk라는 벡터가 1,2,..,k 개 존재합니다.

이렇게 만들어진 K개의 피쳐 맵들은 매핑 모듈에 입력되고, 모듈을 통해 더 representative한 피쳐들로 aggregation합니다. 다만 기존의 방식들로 aggregation할 경우 공간 정보를 잃어버리는 경우가 발생한다고 합니다. 그래서 저자는 Fine-grained structure mapping이라는 방식을 aggregation하기 전에 사용하는 방법을 제안했습니다. 이 방식이 이 논문의 특징으로, FSA-Net의 약자이기도 합니다. 해당 계산 과정은 다음과 같이 동작합니다.

 

1. 이후 설명할 scoring function을 통해 Attention map Ak를 계산합니다.
2. 피쳐 맵 Uk와 어텐션 맵 Ak를 fine-grained structure mapping module에 적용합니다.
3. 이 모듈은 공간적인 가중치를 부여하며 n` c-d 의 피쳐들을 추출하는 법을 학습합니다.
4. 이후 나온 벡터를 feature aggregation method에 적용하여 K c ′-d의 피쳐를 포함하는 벡터 V를 출력합니다.
5. 이 Vk는 FC layer를 통해 k번째 stage에 대한 {~p(k) , ~η(k) , ∆k}를 출력하는 데 사용합니다.
6. 이후 이 출력들은 최종 포즈 추정을 위해 SSR 모듈에 적용됩니다.

정리하자면, FSA라는 기법은 
1)scoreing function, 
2)fine-grained structre mapping, 
3)feature aggregation을 사용하여 기존 피쳐들을 더 representative한 피쳐들로 aggregation합니다.

동작 방법을 제외하고 요약하면, 
FSA라는 기법은 일반적인 피쳐들에 대해 공간적인 정보 등을 포함해 더 대표적인 피쳐들로 aggregation하는 기법입니다.

Scoring function

이 함수는 피쳐들을 그룹화 하는 데 있어 사용되는 함수입니다. 기존 가공 전의 변수를 논문에서는 pixel-level의 변수라고 표현하는데, 이 변수 u가 들어오면 scoring function을 사용하여 공간적인 정보를 활용하기 위해 중요도(또는 어텐션)를 측정합니다. 이 함수를 통해 나온 결과인 Attention Map Ak를 다음과 같이 표현할 수 있습니다.

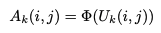
scoring function에는 세 가지 옵션이 존재합니다. 모델은 이 세 가지 옵션 중 하나를 사용하여 작동하게 됩니다. 첫 번째는 1 x 1 Convolution입니다. 해당 레이어를 학습 가능한 scoring function으로 사용합니다. 이를 수식화하면,

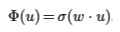
으로 표현할 수 있습니다. 시그모이드 함수를 적용했으며 w라는 가중치는 학습가능한 1 x 1 컨볼루젼망을 말합니다. 다만 트레이닝 셋으로 가중치 부여를 학습하는 데 있어 데이터 셋의 문제로 인한 오버피팅 문제들이 발생할 수 있습니다.

두 번째는 Variance입니다. 말 그대로 변수를 선택하는 데 있어 분산을 사용합니다. 분산은 앞의 1 x 1 Conv처럼 학습 할 수는 없지만 미분 가능하다는 장점이 존재합니다.

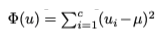
마지막 기능은 Uniform입니다. 쉽게 말해 모든 변수들을 동등한 확률로 사용하는 방법으로, 이 옵션을 사용할 경우에는 fine-grained structure mapping를 수행하지 않게끔 구성되어 있습니다.

저자는 실험 결과 이 옵션들이 서로 다른 측면을 포착한다는 걸 확인했고, 이 각각의 옵션들을 사용한 모델들을 앙상블하는 것을 제안했습니다. 이를 통해 포즈 추정의 성능이 더 높아진다고 합니다.

pixel-level의 변수들을 매핑하기 전에 공간적인 중요도를 측정하기 위해 scoreing function을 사용합니다. 
세가지 옵션 1) 1x1 Conv, 2) Variance, 3) Uniform이 존재하며 모델은 각각을 앙상블하여 사용하고 있습니다.

Fine-grained structure mapping

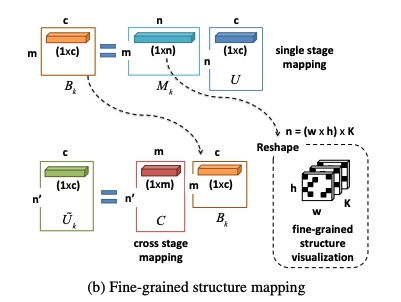
앞의 Overview에서 봤듯이 피쳐 맵 Uk, 그리고 어텐션 맵 Ak를 사용하여 fine-grained structure mapping을 수행하여 최종 피쳐 맵인 U~를 만들게 됩니다. 우선 모든 피쳐 맵 Uk 들에 대해 U로 Flatten하는 과정을 수행합니다. 수식으로 정리하면 다음과 같습니다.

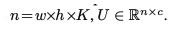
이를 쉽게 표현하면, 기존 w x h x c의 3D 피쳐 맵 Uk들을 모두 합쳐 (w x h) x K개의 행, c개의 열인 2D로 수정하는 것을 말합니다. 여기서 이렇게 만들어진 U를 우리가 원하는 최종 벡터 U~로 매핑하는 방법인 Sk를 찾고 싶다고 가정하면, 이를 다음과 같이 수식화 할 수 있습니다.

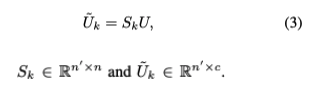
U, Sk, U~k의 차원을 보고 추가로 정리를 하겠습니다. Sk를 통해 기존 n개의 pixel-level 변수를 n`개의 representative한 특징으로 조합할 수 있다는 걸 확인할 수 있습니다. 여기서 Sk는 모든 pixel-level 변수에 대해 가중 평균을 사용하여 차원 축소를 수행하는 이해하기 힘든 어떠한 변환기입니다. 이 Sk를 이해하기 쉽게끔 두개의 학습 가능한 변수로 나눠보겠습니다.

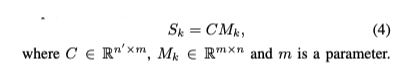
Mk는 각 stage k마다 다른 값이 있을 것이고, C는 모든 k에서 공유되는 특성을 가지고 있습니다. 각각에 대한 수식은 다음과 같습니다.

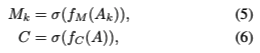
이 안의 함수들은 FC layer로 정의되는 함수들이고, FSA-Net에서 학습을 하며 발견되는 학습가능한 함수입니다. A는 [A1,…,Ak]라는 모든 어텐션 맵의 연결을 말합니다. 이렇게 Sk를 두 개로 분리함으로써 파라미터의 수를 줄이고, 더 안정화할 수 있습니다. 더 안정적이게 트레이닝 하기 위해 Sk의 각 행에 대해 L1 정규화를 수행합니다.

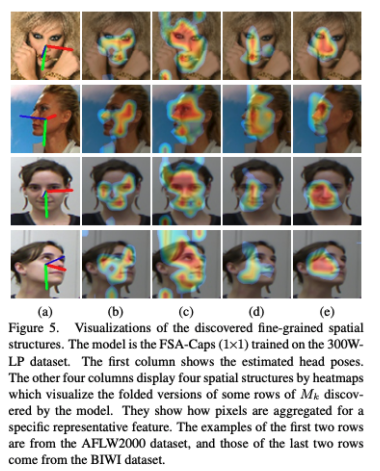
Mk의 각 행은 K개의 맵으로 만들 수 있습니다. (기존 U 가 (w x h) x K개의 행) 각각의 맵들은 어떻게 pixel-level 의 피쳐들이 representative feature에 기여하는지 나타내는데, 그렇기 때문에 결국 Mk의 각 행을 Fine-grained structure라고 볼 수 있습니다. 이에 대한 몇 개를 시각화한 그림을 보여드리겠습니다.

마지막으로 각 U~k들을 U~로 모읍니다. 수식은 다음과 같습니다.

이를 Feature aggregation하면 최종 단계 전인 V 벡터를 구할 수 있게 됩니다.

난해한 내용들이 나오지만 간단하게 요약할 수 있습니다. 
데이터 U가 들어온 후 각 stage별로 공간 정보 등을 추출하기 위해 Mk와 곱해지고, 
이후 stage와 상관 없이 조금 더 부각시키기 위한 용도로 C와 곱해져 더 representative한 변수를 만들 수 있고, 
마지막으로 이들을 모아 최종 V 벡터로 aggregation한 이 모든 과정을 FSA 모듈에서 작업합니다.

Details of the architecture

마지막으로 아키텍쳐 부분을 조금 더 확인해보도록 하겠습니다. DeepCD, SSR-Net과 유사하게 FSA-Net은 two stream 구조를 가지고 있습니다. 각각은 두 개의 간단한 구조로 만들어져 있습니다.

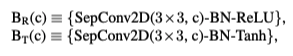
여기서 SepConv2D는 separable 2D conv를 말하며, BN는 배치 정규화를 말합니다. c는 파라미터입니다.

first stream의 경우 {BR(16)-AvgPool(2×2)-BR(32)- BR(32)-AvgPool(2×2)} - {BR(64)-BR(64)-AvgPool(2×2)} - {BR(128)-BR(128)}의 구조를 가지고 있습니다. 여기서 -는 stage라고 생각하면 됩니다.

second stream은 {BT(16)-MaxPool(2×2)-BT(32)-BT(32)-MaxPool(2×2)} - {BT(64)-BT(64)-MaxPool(2×2)} - {BT(128)-BT(128)} 구조입니다. FSA-NET에서 K를 3으로 두고 아키텍쳐를 고정한 것 같습니다.

이외의 파라미터는 다음과 같이 고정했습니다. 피쳐 맵에서 w=8, h=8, c=64, Fine-grained structure에서 m=5, n=7, c=16

Experiments

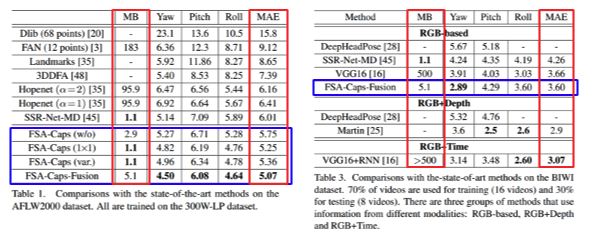
타 모델들에 비해 좋은 성능을 보이고 있습니다. Fusion이라고 써진 부분이 위의 3개 모델을 합친 최종 모델입니다.

Reference & Demo

저자의 깃헙에서 Demo를 공개했습니다. shamangary/FSA-Net

데모에 대해 주석과 몇가지 설명을 추가 정리한 Repo입니다. saeu5407/FSA-Net