고유값(eigen value)와 고유벡터(eigen vector)
0이 아닌 어떤 열벡터 v가 있다고 생각해보자.
v를 기준으로, 어떤 A라는 정방행렬과의 연산을 취하면 원래와는 다른 벡터 b가 나오게 된다.
Av = b
하지만 어떤 특정한 행렬은 기존 벡터와 평행하지만 크기만 다른 벡터가 나오게 된다.
Av = Λv
이 상황은 정방행렬과 어떤 벡터와의 연산은 그 벡터에 대해 상수배를 취한 것과 같다로 정리할 수 있다.
여기서 상수 Λ를 고유값(eigen value), 벡터 v를 고유벡터(eigen vector)라고 한다.
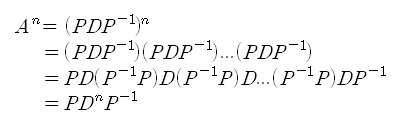
거듭제곱의 단순화처럼, 행렬 A에 대해 고유값, 고유벡터를 찾음으로써 문제 해결의 복잡도를 단순화 시킬 수 있다는 장점이 있다.
주성분분석에서의 활용
주성분분석 관점에서 고유값과 고유벡터를 생각해보자.
우리가 풀고자 하는 어떤 다차원의 데이터(X)의 공분산행렬 A를 구해보자.
A는 정방행렬이며, 대칭행렬이다.
해당 A에 대해 위의 식을 대입하면 Av = Λv 로 분해할 수 있다.
참고에 있는 Var(z1) = Λ1(z1은 고유벡터를 투영한 새로운 변수) 등 증명을 통해 공식들을 적용해 보면
(1) 고유값이 새로운 변수가 가진 분산과 같다는 결과와,
(2) 이를 확장하여 원데이터의 분산이 고유값의 전체 합과 같다는 결과,
(3) A가 대칭행렬임을 이용하여 고유벡터끼리 상관성이 없다는 결과를 얻을 수 있다.
결론적으로 고유값과 고유벡터를 활용한 주성분분석을 통해,
(1) 원 데이터의 분산을 대부분 보존하면서도 더 적은 차원으로 줄일 수 있다.
(2) 다중공선성등 변수간의 상관성이 있을 때 이를 해결하기 위한 방법으로도 사용할 수 있다.
공식(출처1), 응용(출처2)
출처1 : https://ratsgo.github.io/machine%20learning/2017/04/24/PCA/
출처2 : https://blog.daum.net/jungjin1980/148
고유값(eigen value)와 고유벡터(eigen vector)
0이 아닌 어떤 열벡터 v가 있다고 생각해보자.
v를 기준으로, 어떤 A라는 정방행렬과의 연산을 취하면 원래와는 다른 벡터 b가 나오게 된다.
Av = b
하지만 어떤 특정한 행렬은 기존 벡터와 평행하지만 크기만 다른 벡터가 나오게 된다.
Av = Λv
이 상황은 정방행렬과 어떤 벡터와의 연산은 그 벡터에 대해 상수배를 취한 것과 같다로 정리할 수 있다.
여기서 상수 Λ를 고유값(eigen value), 벡터 v를 고유벡터(eigen vector)라고 한다.
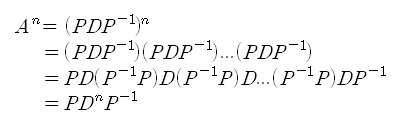
거듭제곱의 단순화처럼, 행렬 A에 대해 고유값, 고유벡터를 찾음으로써 문제 해결의 복잡도를 단순화 시킬 수 있다는 장점이 있다.
주성분분석에서의 활용
주성분분석 관점에서 고유값과 고유벡터를 생각해보자.
우리가 풀고자 하는 어떤 다차원의 데이터(X)의 공분산행렬 A를 구해보자.
A는 정방행렬이며, 대칭행렬이다.
해당 A에 대해 위의 식을 대입하면 Av = Λv 로 분해할 수 있다.
참고에 있는 Var(z1) = Λ1(z1은 고유벡터를 투영한 새로운 변수) 등 증명을 통해 공식들을 적용해 보면
(1) 고유값이 새로운 변수가 가진 분산과 같다는 결과와,
(2) 이를 확장하여 원데이터의 분산이 고유값의 전체 합과 같다는 결과,
(3) A가 대칭행렬임을 이용하여 고유벡터끼리 상관성이 없다는 결과를 얻을 수 있다.
결론적으로 고유값과 고유벡터를 활용한 주성분분석을 통해,
(1) 원 데이터의 분산을 대부분 보존하면서도 더 적은 차원으로 줄일 수 있다.
(2) 다중공선성등 변수간의 상관성이 있을 때 이를 해결하기 위한 방법으로도 사용할 수 있다.
공식(출처1), 응용(출처2)
출처1 : https://ratsgo.github.io/machine%20learning/2017/04/24/PCA/
출처2 : https://blog.daum.net/jungjin1980/148
